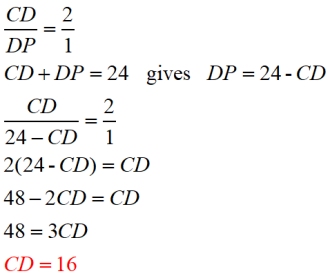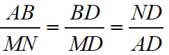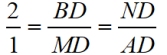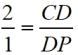Things to remember before we begin:
• The "centroid" of a triangle is the point of concurrency
for the three medians of the triangle.
• The median of a triangle connects a vertex to the midpoint of the opposite side.
• A point of concurrency is the point where all three medians intersect.

The "Centroid" Theorem says that the location of the point, called the centroid, divides each of the medians of the triangle into a ratio of 2:1. The longer portion of the median will be connected to the vertex of the triangle.

example

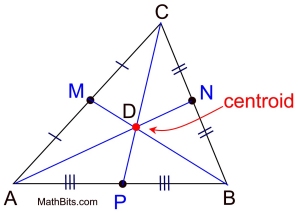
Given diagram shown.
If CP = 24", find CD.




After finding the answer, we can
see that CD : DP = 16 : 8 = 2 : 1.

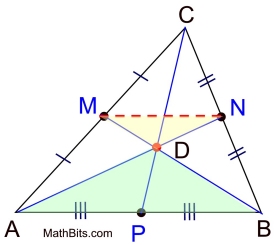
The diagram shows ΔABC with all 3 medians drawn and centroid (point D) labeled.
CP = 24"

dividerdash

Theorem2
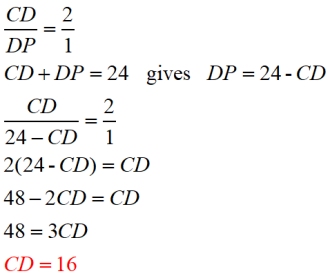
(Centroid Theorem): The centroid of a triangle divides each median in the ratio 2 : 1. (proof below)
The proof of this theorem will concentrate on establishing ratios
(AD : DN and BD : DM) to be equivalent to 2 : 1.
The other median ratio can follow this same procedure.
  Proof:
Statements
Reasons
1. D centroid, midpts M,N,P
1. Given
2.
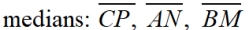2. Median of a Δ connects the vertex to the midpoint of the opposite side.
3. Connect midpoint M to midpoint N
3. Two points determine one, and only one straight line.
4.
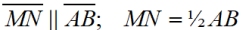4. The mid-segment of a Δ (connecting the midpts of two sides) is || to the 3rd side and ½ the 3rd side.
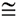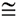5. ∠NMB congruent∠MBA
    ∠MNA congruent∠NAB
5. If 2 || lines are cut by a transversal, the alternate interior angles are congruent.
6. ΔMND ΔBAD
6. AA: If 2 ∠s of one Δ are 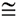congruent to the corresponding ∠s of another Δ, the Δs are similar.
7.
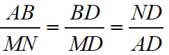7. Corresponding side of similar triangle are in proportion.
8.
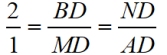8. Substitution (from step 4)
9. 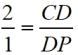9. Repeat this process connecting point M to point P.

 


divider


NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".