 |
Remember -- use your compass
and straightedge only! |
|
Dilations: Similar Triangles |
|
The simplest dilation to construct is the dilation associated with similar triangles where one side of the image triangle is given. Let's take a look.
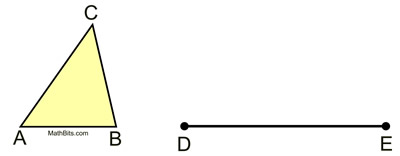
Given: Δ ABC and segment from D to E
Construct: a triangle similar to Δ ABC,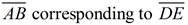
|
|
STEPS:
1. Copy ∠A at point D.
2. Copy ∠B at point E.
3. Draw each of the angles until they intersect at point F.
4. 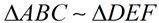
(by Angle-Angle, AA) |
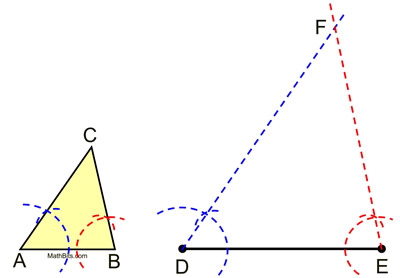 |
Proof of Construction: The copies made of angles A and B give us ∠A  ∠D and ∠B ∠D and ∠B  ∠E. Hence, ΔABC is similar to ΔDEF, since two triangles are similar if two angles of one triangle are congruent respectively to two angles of the other triangle. ∠E. Hence, ΔABC is similar to ΔDEF, since two triangles are similar if two angles of one triangle are congruent respectively to two angles of the other triangle.
Dilations: Given Scale Factor |
Dilation constructions are not always as simple as the one shown above.
A dilation is often described by the scale factor and the center of the dilation.
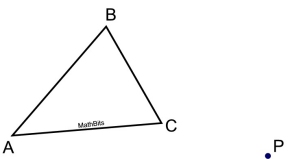
Consider this example.
Given: ΔABC and point P
Construct: the dilation of ΔABC by a scale factor of 2 centered at point P
|
|
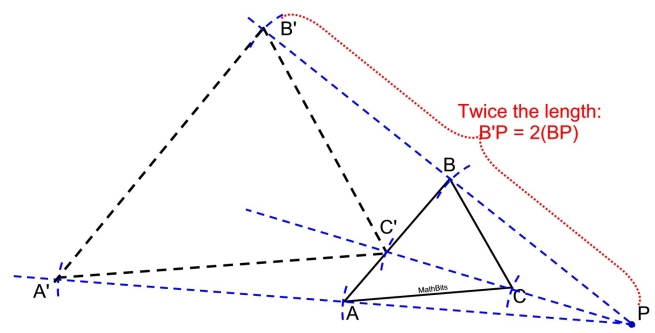 |
STEPS:
1. Draw lines from point P through each of the vertices of the triangle. Extend lines beyond the triangle.
2. Measure the length from P to B. Place compass point on B and copy this distance on the line through B and P. Label B'.
3. Repeat this process for vertices C and A.
4. Draw ΔA'B'C' (It is not always the case that the new triangle will touch, or be inside, the given triangle.) |
If the scale factor is a different integer value, such as 3,
simply copy the length BP, along the line 3 times from point P
(in regards to the construction shown above)
.
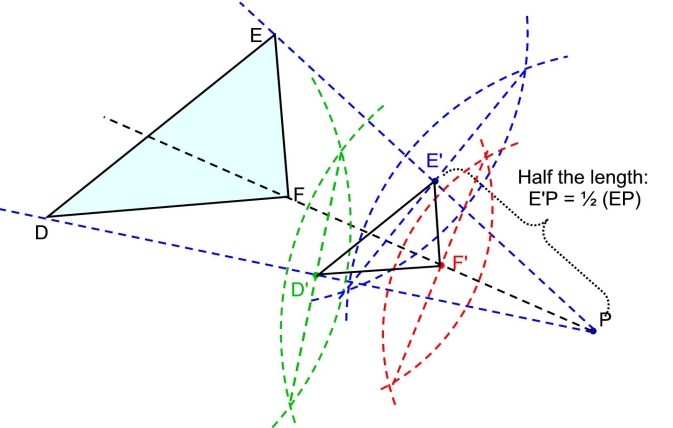
If the scale factor is a fraction, such as ½, you will need to bisect the distance
from P to each vertex point,
to obtain a measurement for a ½ scale factor.
See construction below.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|





