|
Transformational Definition:
|
Two figures are congruent if and only if there exists one, or more, rigid transformations which will map one figure onto the other. |
|
| Rigid transformations are:
| |
• reflections |
| |
• translations |
| |
• rotations |
|
|
|
Rigid transformations can be called:
| |
• isometries |
| |
• congruence transformations |
| |
• rigid motions |
|
|
Rigid transformations move figures to a new location without altering their size or shape
(thus maintaining the conditions for the figures to be congruent).
If figures are congruent, the corresponding sides are congruent,
and the corresponding angles are congruent.
To show that figures are congruent using rigid transformations,
you must establish a way to map the pre-image figure onto the resulting image
using rigid transformations. |
Using Rigid Transformation(s) to Determine Congruence:
|
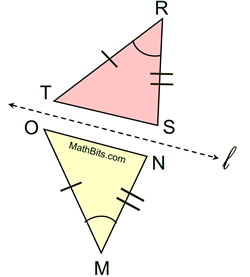
Given the triangles positioned and marked as shown with a set of sides being parallel.
Is ΔRST  ΔMNO? ΔMNO?
Consider ΔRST to be the pre-image.
By the definition of congruent, we need to find a rigid transformation that will map ΔRST onto ΔMNO.
Rigid transformation: Reflection
Establish a reflection line l half-way between the triangles, as shown, over which ΔRST can be mapped to coincide with ΔMNO.
Thus, ΔRST  ΔMNO. ΔMNO. |
|
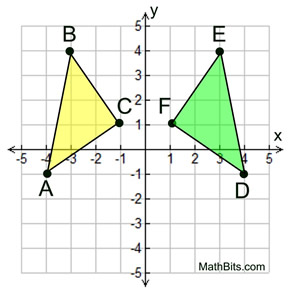
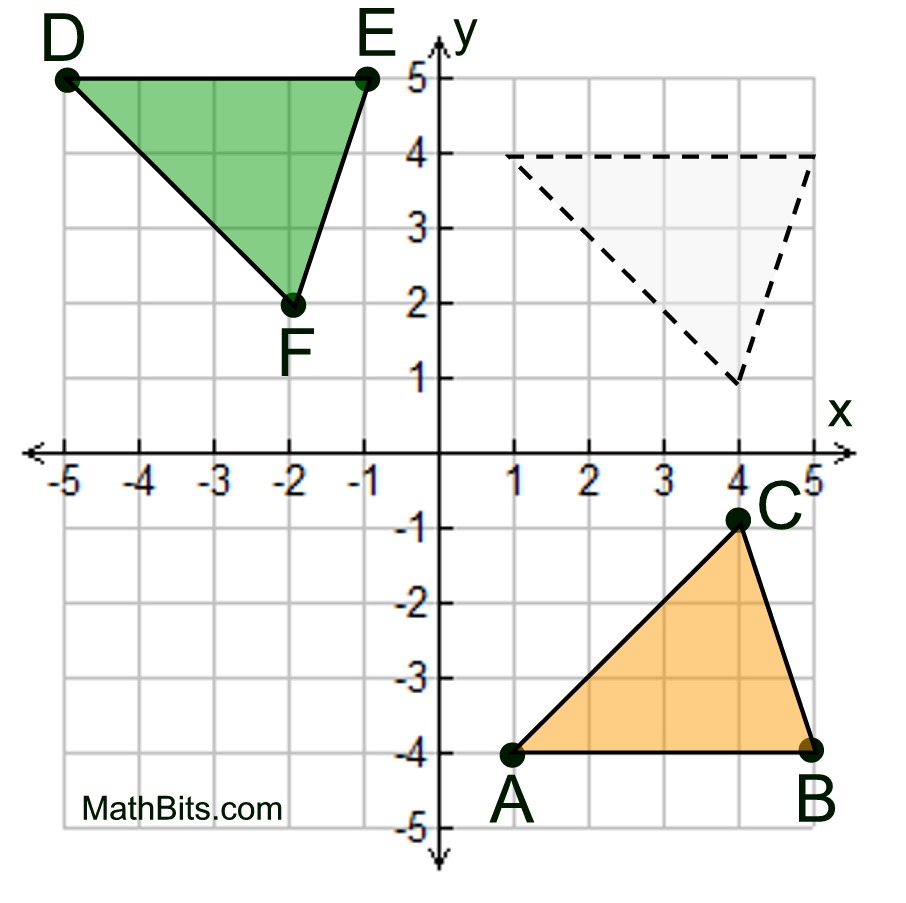
Given the graph at the left.
Is ΔABC  ΔDEF? ΔDEF?
Consider ΔABC to be the pre-image.
By the definition of congruent, we need to find a rigid transformation that will map ΔABC onto ΔDEF.
Rigid transformation: Reflection
A reflection over the y-axis will map Δ ABC to coincide with Δ DEF, making
ΔABC 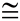 ΔDEF. ΔDEF. |
|
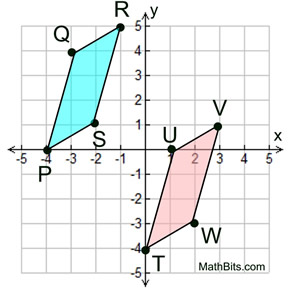
Given the graph at the left.
Is  PQRS PQRS 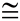  TUVW?
Consider parallelogram PQRS to be the pre-image. TUVW?
Consider parallelogram PQRS to be the pre-image.
We need to find a rigid transformation that will map one parallelogram onto the other.
Rigid transformation: Translation
The translation ( x, y) → ( x + 4, y - 4) will map PQRS onto TUVW, making
 PQRS PQRS 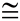  TUVW. TUVW. |
|
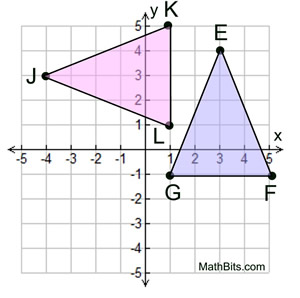
Given the graph at the left.
Is ΔEFG 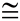 ΔJKL? ΔJKL?
Consider ΔEFG to be the pre-image.
We need to find a rigid transformation that will map one triangle onto the other.
Rigid transformation: Rotation
A rotation of 90º CCW about the origin will map Δ EFG to coincide with Δ JKL, making
ΔEFG 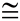 ΔJKL. ΔJKL. |
|
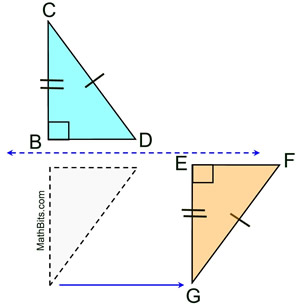
Given the diagram at the left.
Is ΔBCD 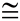 ΔEFG? ΔEFG?
Consider ΔBCD to be the pre-image.
Rigid transformations: Reflection and Translation (Sometimes a combination of rigid transformations is needed to map one figure onto another.)
Assuming 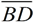 and and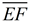 are horizontal, reflect ΔBDC over a horizontal line halfway between are horizontal, reflect ΔBDC over a horizontal line halfway between 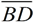 and and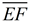 . Then translate the image horizontally to the right to coincide with ΔEFG making ΔBCD . Then translate the image horizontally to the right to coincide with ΔEFG making ΔBCD 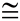 ΔEFG. ΔEFG. |
|
Given the graph at the left.
Is ΔABC 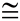 ΔDEF? ΔDEF?
Consider ΔABC to be the pre-image.
We need to find a combination of rigid transformations that will map one triangle onto the other.
Rigid transformations: Reflection and Translation
A reflection in the x-axis, followed by a translation of ( x, y) → ( x - 6, y + 1), will map Δ ABC to coincide with Δ DEF, making
ΔABC 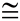 ΔDEF. ΔDEF. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|