|
Transformations are used to move and resize graphs of functions.
We will be examining the following changes to f (x):
- f (x), f (-x), f (x) + k, f (x + k), kf (x), f (kx)
reflections translations dilations
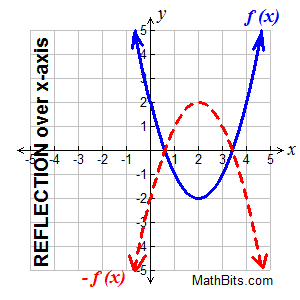
Reflections of Functions: -f (x) and f (-x) |
 Reflection over the x-axis.
-f (x) reflects f (x) over the x-axis
|
|
Reflections are mirror images. Think of "folding" the graph over the x-axis.
On a grid, you used the formula
(x,y) → (x,-y) for a reflection in the
x-axis, where the y-values were negated. Keeping in mind that y = f (x),
we can write this formula as
(x, f (x)) → (x, -f (x)). |
 |
|
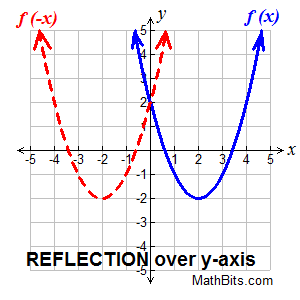
Reflection over the y-axis.
f (-x) reflects f (x) over the y-axis |
|
Reflections are mirror images. Think of "folding" the graph over the y-axis.
On a grid, you used the formula (x,y) → (-x,y) for a reflection in the y-axis, where the x-values were negated. Keeping in mind that
y = f (x), we can write this formula as
(x, f (x)) → (-x, f (-x)).
|
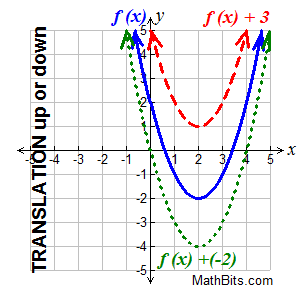
Translations of Functions: f (x) + k and f (x + k) |
Translation vertically (upward or downward)
f (x) + k translates f (x) up or down |
|
This translation is a "slide" straight up or down.
• if k > 0, the graph translates upward k units.
• if k < 0, the graph translates downward k units.
On a grid, you used the formula (x,y) → (x,y + k) to move a figure upward or downward. Keeping in
mind that y = f (x), we can write this formula as (x, f (x)) → (x, f (x) + k).
Remember, you are adding the value
of k to the y-values of the function. |
 |
|
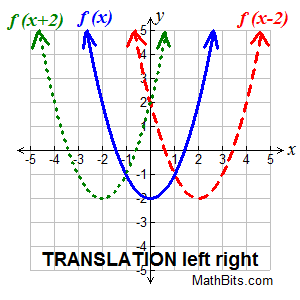
Translation horizontally (left or right)
f (x + k) translates f (x) left or right |
|
This translation is a "slide" left or right.
• if k > 0, the graph translates to the left k units.
• if k < 0, the graph translates to the right k units.
This one will not be obvious from the patterns you previously used when translating points.
A horizontal shift means that every point ( x,y) on the graph of f ( x) is transformed to ( x - k, y) or ( x + k, y) on the graphs of y = f ( x + k) or y = f ( x - k) respectively.
Look carefully as this can be very confusing!
|
Hint: To remember which way to move the graph, set (x + k) = 0. The solution will tell you in which direction to move and by how much.
f (x - 2): x - 2 = 0 gives x = +2, move right 2 units.
f (x + 3): x + 3 = 0 gives x = -3, move left 3 units. |
|
|
| Dilations of Functions: kf (x) and f (kx) |
Vertical Stretch or Compression (Shrink)
k f (x) stretches/shrinks f (x) vertically |
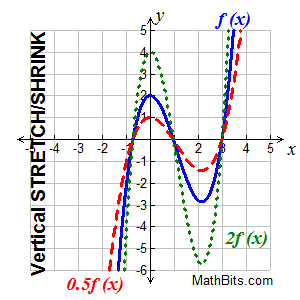
"Multiply y-coordinates"
(x, y) becomes (x, ky)
"vertical dilation"
|
A vertical stretching is the stretching of the graph away from the x-axis
A vertical compression (or shrinking) is the squeezing of the graph toward the x-axis.
• if k > 1, the graph of y = k•f (x) is the graph of f (x) vertically stretched by multiplying each of its y-coordinates by k.
• if 0 < k < 1 (a fraction), the graph is f (x) vertically shrunk (or compressed) by multiplying each of its x-coordinates by k.
• if k should be negative, the vertical stretch or shrink is followed by a reflection across the x-axis.
Notice that the "roots" on the graph stay in their same positions on the x-axis. The graph gets "taffy pulled" up and down from the locking root positions. The y-values change. |
|
|
Horizontal Stretch or Compression (Shrink)
f (kx) stretches/shrinks f (x) horizontally |
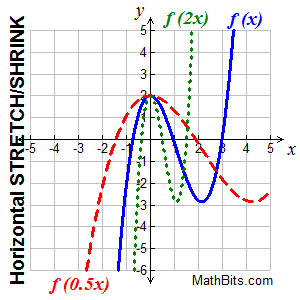
"Divide x-coordinates"
(x, y) becomes (x/k, y)
"horizontal dilation"
|
A horizontal stretching is the stretching of the graph away from the y-axis
A horizontal compression (or shrinking) is the squeezing of the graph toward the y-axis.
• if k > 1, the graph of y = k•f (x) is the graph of f (x) horizontally shrunk (or compressed) by dividing each of its x-coordinates by k.
• if 0 < k < 1 (a fraction), the graph is f (x) horizontally stretched by dividing each of its x-coordinates by k.
• if k should be negative, the horizontal stretch or shrink is followed by a reflection in the y-axis.
| Notice that the "roots" on the graph have now moved, but the y-intercept stays in its same initial position for all graphs. The graph gets "taffy pulled" left and right from the locking y-intercept. The x-values change. |
 |
|
Transformations of Function Graphs |
|
reflect f (x) over the x-axis
|
f (-x) |
reflect f (x) over the y-axis |
f (x) + k |
shift f (x) up k units |
f (x) - k |
shift f (x) down k units |
f (x + k) |
shift f (x) left k units |
f (x - k) |
shift f (x) right k units |
k•f (x) |
multiply y-values by k |
f (kx) |
divide x-values by k |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
