The lesson "Intro to Inverses of Functions" gave us a glimpse of working with inverse functions.

This lesson will concentrate specifically on the inverse relationship
between exponential and logarithmic functions, both graphically and algebraically,

Graphically:
 

We have seen inverse graphs at work. Basically, to find the inverse of a function, the inputs (x) and outputs (y) exchange places. Graphically, the inverse will be a reflection of the original graph over the identity line y = x (also called the Identity Function).

As this relates to exponential and logarithmic functions, we have seen that:
f (x) = 2x
x
-2
-1
0
1
2
3
f(x)
¼
½
1
2
4
8

The inverse: f -1 (x)
x
¼
½
1
2
4
8
f-1(x)
-2
-1
0
1
2
3

y = log2 (x) is the inverse of  y = 2x
and y = 2x is the inverse of  y = log2 (x)
loginverse

dividerdash

We have seem the connection between "composition of functions" and "inverse functions".
When working with inverse functions, the following statements are true:
f (f -1(x)) = x           and also in reverse        f -1(f (x)) = x
The composition returns the x-value of the starting function, creating the identity line y = x.

A function composed with its inverse creates the identity line y = x. 

Since exponential functions and logarithmic functions are inverses we can write: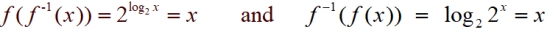 

The graphing calculator can quickly show whether the composition of two functions creates the Identity Function y = x, thus making the two functions inverses of one another. 

The exponential function "composed" with the logarithmic function creates the line y = x.

dividerdash

FYI: The inverse function of a logarithm is called an antilogarithm (or antilog).
Given: y = log10(x), then antilog(y) = 10y = x.

Shouldn't we just call the inverse of a logarithm an "exponential" ?
Yes, we can. But, when logarithms first came on the scene, they were not associated with exponentials, thus the word "antilogarithm". Their association with exponentials was established later.

dividerdash


Let's take a look at the graphs when 0 < b < 1, such as b = 0.5.
Exponential function, g(x), and logarithmic function, g-1(x):

g(x) = 0.5x
x
-2
-1
0
1
2
3
g(x)
4
2
1
1/2
1/4
1/8

The inverse: g -1(x)
x
4
2
1
1/2
1/4
1/8
g-1(x)
-2
-1
0
1
2
3

y = log0.5 (x) is the inverse of  y = 0.5x
and y = 0.5x is the inverse of  y = log0.5 (x)

exgraph5

dividerdash

Algebraically:
 

Let's solve algebraically for the Inverses that were investigated above:

Remember:
Graph
Inverse
Graph
Inverse
ex3
ex4
ex5
ex6
y = 2x
• set the equation equal to y
x = 2y
• swap the x and y
y = log2x
• solve for y by rewriting in log form
y = 0.5x
• set the equation equal to y
x = 0.5y
• swap the x and y
y = log0.5x
• solve for y by rewriting in log form

Alternate method of finding an inverse algebraically:
hintgal
altlog
set the equation equal to y

swap the x and y variables

take the log of both sides

apply the rule: log ar = r log a

solve for y

apply the Change of Base Formula:
logb a = log a / log b




How to use your graphing calculator for working
with
logarithms
Click here.
ti84c
How to use
your graphing calculator for
working
with
logarithms,
Click here.


divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".