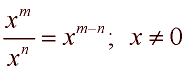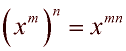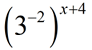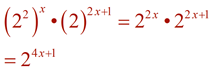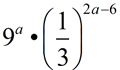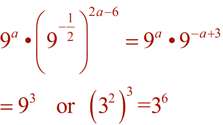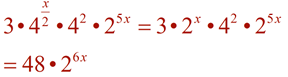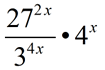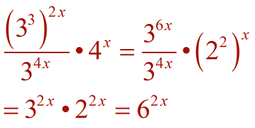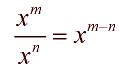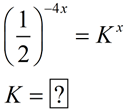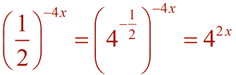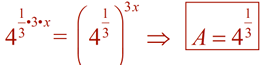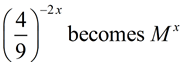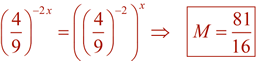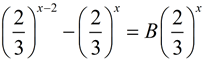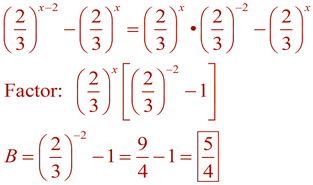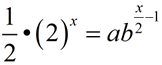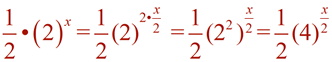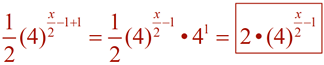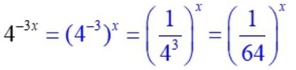bullet An exponential expression is one which contains an exponent.
It is a mathematical way to show repeated multiplication, in a short form (i.e., 23).
The form is a base number (or variable) raised to a value called the exponent.

We will be focusing on exponential expressions of the form bx,
where the base is a constant and the exponent is a variable.

In relation to "functions", there is a difference in "naming" 2x and x2.
f (x) = 2x is an exponential function, while f (x) = x2 is a power function.

When working with exponential expressions, you will need to remember the rules that pertain to dealing with exponents. Algebra 2 will expect you to use these rules (forward and backward) in a variety of situations. Primarily, you will need to remember the following rules:

Product Rule: prodrule
Quotient Rule:
quotrule
Power to Power Rule:
powerrulw
Product to Power Rule:
pprule


Simplifying Exponential Expressions:
 
Simplify the following expressions into the form a•bx.
1.
 ee1 Solution:    ee1a Rule: prodrule
2.
 dd2 Solution:     ee2a Rule: powerrulw
3.
 ee31 Solution:  Get a common base.  ee3a Rule: powerrulw
Rule: prodrule
4.
 ee41 Solution: Get a common base.
  ee4a		 Rule: powerrulw
Rule: prodrule
5.
 ee5 Solution: Simplify 2nd term.   
ee5a		 Rule: powerrulw
Rule: prodrule
6.
 ee6 Solution:   Simplify quotient.  ee6a

Rule: powerrulw
Rule: shrule
Rule: pprule




Re-writing Exponential Expressions and Equations:
 
You may be asked to re-write an exponential expression in a simpler form, as seen above, to make it more easily readable. Or you may be asked to re-write the expression into a more obscure form to reveal pertinent information about a concept or about the expression itself.
1.
 Find K.
rw1
 Solution:   Let's see if we can re-write the left-hand side to contain an exponent of simply x.
rw1a
Better, but not good enough. If we cannot simplify the left-side further, how can we manipulate what we have into becoming K x ?
rw1aa
2.
 To rewrite
rw2a,
A will be _____.
 Solution:    We need the exponent on 4 to contain a 3. We can introduce 3•1/3 (which equals 1) without changing the expression.
rw2aa1
3.
 Find M, such that
rwaa		 Solution:   Separate the exponent to produce the x alone.
 rw3a
4.
 Find B.rw4 Solution:  Re-write the first term and then factor. 
rw4a  
5.
 Find a and b:
rw55		 Solution: Yikes! Let's work on that exponent first. rw5a  
OK, so far, so good. Now, work on the -1 by adding a 0 as -1+1.
rw5aa
a = 2 and b = 4



Manipulating Exponential Expressions to find "b"

In Algebra 2, our focus is on exponential functions of the form  f (x) = abx.

The form,  f (x) = abx , utilizes bx where the value of b gives important information about the function and its graph. In certain situations, we may need to rewrite an exponential expression such that the only exponent is x, allowing us to "see" the base value as b.

Using the "Power to a Power" property of exponents, (xm)n = xmn , in reverse, re-write the following expressions into a form bx, maintaining only "x" as the exponent, with a real number value for b.

Example 1:

If f (x)= 52x, we now know that the value
of b is 25.

 

 Example 2:
If g(x)= 4-3x, we know that the value
of b is 1/64.


divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".