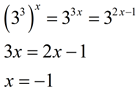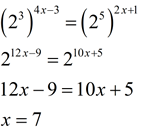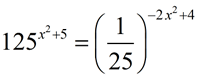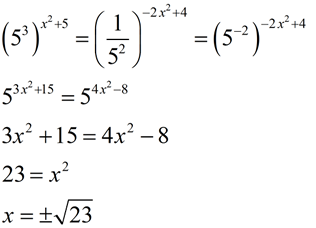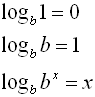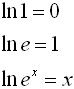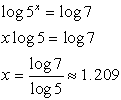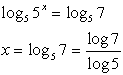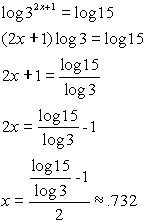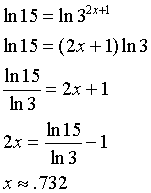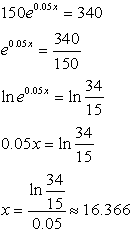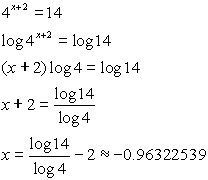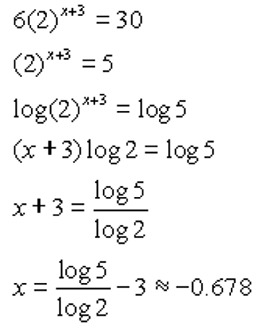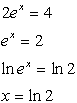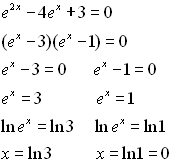We will examine two algebraic methods for solving exponential equations:
1. Using a Common Base (while a "nice" method, its applications are limited)
2. Using Logarithms (a more universal solution method)

NOTE: for a graphical solution, follow the calculator link at the bottom of this page.

Solution Method 1: Using a Common Base An exponential equation in which each side can be expressed in terms of the same base can be solved using this property: if bx = by, then x = y (where b > 0 and b ≠1). If the bases are the same, set the exponents equal.

	Solve for x:	Answer
1.		Since the bases are the same, set the exponents equal to one another and solve for x: 3x - 2 = 2x + 1 x = 3
2.		27 can be expressed as a power of 3:
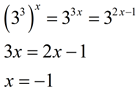
3.		Both 8 and 32 can be expressed as powers of 2:
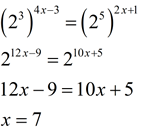4.		Both 125 and 1/25 can be expressed as powers of 5: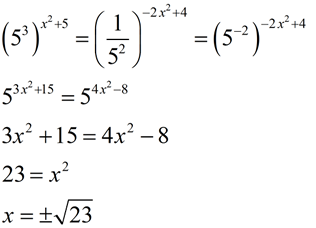
5.	2x = -8	Stop! Don't bother writing -8 as -(23) as it doesn't help. The negative sign still remains in the base. There is NO common base. This equation has no real solutions. Remember the look of the graph of 2x. It resides in quadrants I and II, asymptotic to the x-axis. This function never yields negative y-values.

Inverse Relationships:
The composition of a function with its inverse returns the starting value, x.

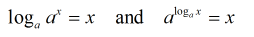
ln(e^x) = x    and    e^ln(x) = x
This concept will be used to solve equations involving exponentials and logarithms.

Unfortunately, not all exponential equations can be expressed in terms of a common base. For these equations, logarithms are used to arrive at a solution. (You may solve using common log or natural ln, but when working with e, use ln.)

Remember:

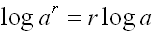
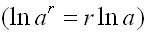Solution Method 2: Using logs To solve most exponential equations: 1.  Isolate the exponential expression. 2.  Take log or ln of both sides, to set up the inverse relationship between exponentials and logarithms. 3.  Apply the inverse relationship. 4.  Solve for the variable.

Things to remember about logs:

Grab your calculator!

	Solve for x, to nearest thousandth:	Answer
1.	5x = 7 * Can you see how trying to get a common base for 5 and 7 would be an extremely difficult task? The log method will save us a good deal of aggravation on this problem. Also notice that the solution can be found using either log or log5.	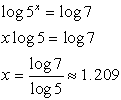OR 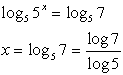• Take the log of both sides. • Apply the log power rule. • Solve for x. • Estimate answer from calculator   • log base 5 can also be used as a solution method. • notice how the log5 of 5x is really composition of inverses and yields x. • Notice the change of base formula used at the end, if needed for older calculators.
2.	15 = 32x+1	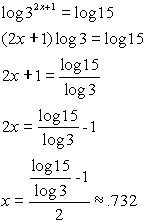OR
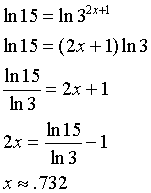3.	ex = 43	Since the natural log is the inverse of the natural exponential function, use ln to quickly solve this problem. ln ex = ln 43 x = ln 43 ≈ 3.761
4.		• First, get rid of the coefficient of the exponential term (divide by 150). • Now, proceed using ln to quickly solve. • Do not round too quickly.  Be sure to carry enough decimal values to allow you to round to thousandths (in this case) for the final answer.
5.		• Isolate the exponential • Take the log of both sides • Apply the log property • Divide by log 4 • Estimate using calculator
6.		• First, divide by the coefficient to isolate the exponential • Take the log of both sides • Apply the log rule • Divide by log 2 • Estimate answer
7.		• Isolate the exponential • Divide each side by the coefficient of 2 • Take ln of both sides • Remember that ln x and ex are inverse functions.
8.		This question requires some additional thinking. Because of the differing powers of e, our previous methods will not be of much help. We will need a different strategy for this problem. 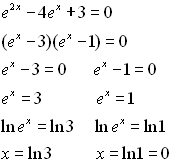• Remember that ex • ex = e2x • This problem is really x2 - 4x + 3 = 0 where x = ex • Factor • Both solutions are answers.

For help with exponential equations on the calculator, Click here.

For help with exponential equations on the calculator, Click here.

Topical Outline | Algebra 2 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
Terms of Use    Contact Person: Donna Roberts