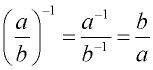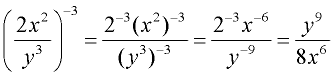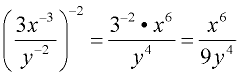This expanded version shows how each factor of the quotient is raised to the new power.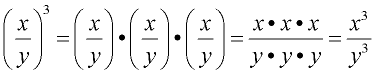
Consider this interpretation using a negative exponent in the quotient.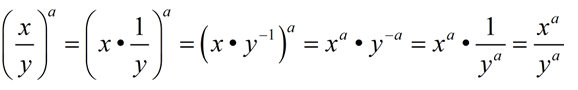
1. 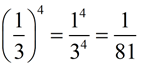
Notice that the exponent is applied to both the numerator and the denominator. |
2. 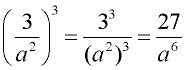
This problem also involves using the "power to a power" rule for (a2)3 = a6.
|
3. 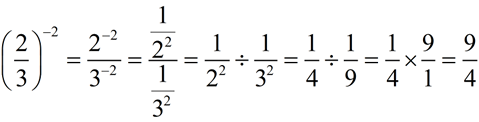
When working with a negative exponent, you can apply the exponent step-by-step, as shown here.
Remember that an answer does not contain a complex fraction (a fraction over another fraction).
|
4. Applying a negative exponent in a step-by-step process.
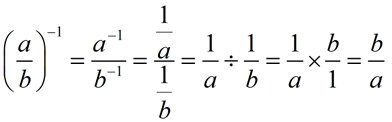 Did you notice in this problem that raising a fraction to a negative one power, flipped the fraction over? Did you notice in this problem that raising a fraction to a negative one power, flipped the fraction over?
|
5. Applying a negative exponent by remembering that the negative exponent means the term in on the wrong side of the fraction bar.
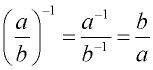 |
6. 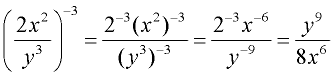
Notice how the negative sign is being handled with the product in the numerator. Each term of the product is raised to -3 power. |
7. 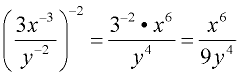
A negative power raised to a negative power is a positive power. Again, notice how the numerator product is being handled.
|


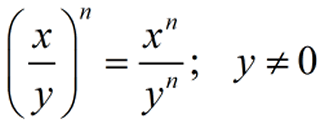

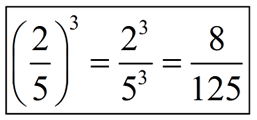
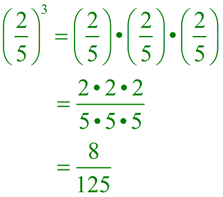
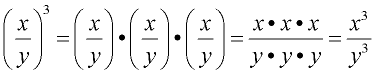
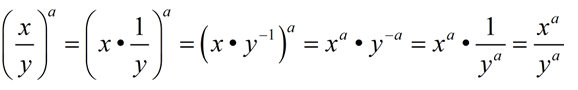
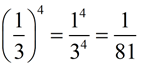
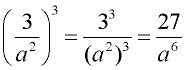
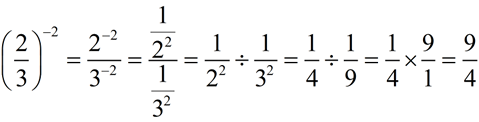
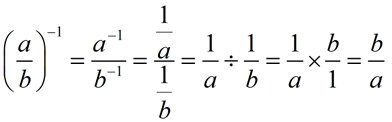 Did you notice in this problem that raising a fraction to a negative one power, flipped the fraction over?
Did you notice in this problem that raising a fraction to a negative one power, flipped the fraction over?