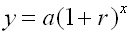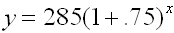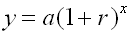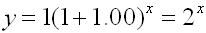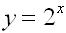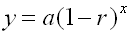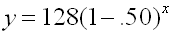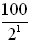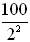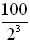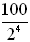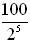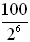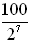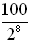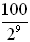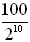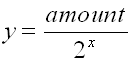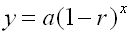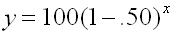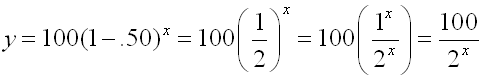|
Exponential functions are of the form y = a(b)x. |
|
Exponential Growth:
y = a(1 + r)x |
|
Exponential Decay:
y = a(1 - r)x |
|
a = initial amount before measuring growth/decay
r = growth/decay rate (often a percent expressed as a decimal)
x = number of time intervals that have passed.
Let's examine rate of growth and decay in a three step process.
(1) build a percent of growth chart to examine the data and "see" the growth or decay,
(2) write an exponential function based upon the data, and
(3) prepare a scatter plot of the data along with the graph of the function.
Obviously, this 3-step method is not "required" in the solution to these problems.
It is used here to show how the data is developing and the relationship to the formula.
 When working with exponential growth and decay, the problem may involve entities that cannot be expressed as fractional parts. For example, when dealing with populations, you cannot conclude that the population will increase by 40.2 people per year. Read carefully, and make sure your answer makes logical sense. When working with exponential growth and decay, the problem may involve entities that cannot be expressed as fractional parts. For example, when dealing with populations, you cannot conclude that the population will increase by 40.2 people per year. Read carefully, and make sure your answer makes logical sense. |

Growth:
Past History
of Cell Phone Users |
In 1985, there were 285 cell phone subscribers in the small town of Centerville. The number of subscribers increased by 75% per year after 1985. How many cell phone subscribers were in Centerville in 1994?
(Don't consider a fractional part of a person.) |
(Manually multiply each previous number of users by 1.75, which is all of them plus 75% more.)
Years
1985 x = 0 |
x = 1
1986 |
2
1987 |
3
1988 |
4
1989 |
5
1990 |
6
1991 |
7
1992 |
8
1993 |
9
1994 |
Number of
Cell Phone users (285) |
498 |
872 |
1527 |
2672 |
4677 |
8186 |
14325 |
25069 |
43871 |
Determined by percent increase chart: There are 43871 subscribers in 1994.
Function: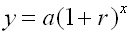 |
a = the initial amount before the growth begins (285)
r = growth rate (75% = 0.75)
x = the number of intervals |
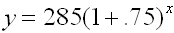 |
as x ranges from 1 to 9 for this problem |
Determined by exponential function: 1994 was 9 years after 1985.
y = 285(1 + 0.75)9 = 43871 whole peoople
The scatter plot of the data table can be prepared by hand or with the use of a graphing calculator.
For graphing the function, employ your graphing calculator.
 |
See how to prepare a scatter plot of your data table using your TI 84+ family of graphing calculators. Click here.
After the data points are plotted, set Y1 = to the function, and graph. The function and the scatter plot will overlap as they did at the
right. |
|
|
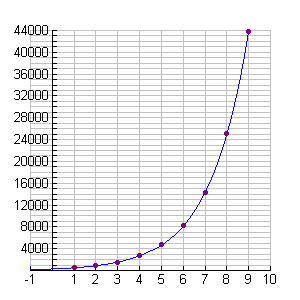
horizontal axis = year (1986 = 1)
vertical axis = number of cell phone users
The y-intercept is (0,128). |
Notice how quickly the graph increased and how large the values on the y-axis became.
Keep in mind that in reality, population growth is seldom, if ever, exactly predictable. |
|

Growth by doubling:
Bacteria
|
One of the most common examples of exponential growth deals with bacteria. Bacteria can multiply at an alarming rate when each bacteria splits into two new cells, thus doubling. For example, if we start with only one bacteria which can double every hour, by the end of one day we will have over 16 million bacteria. |
| End of Hour |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
... |
24 |
Bacteria -
starting with one |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
2048 |
4096 |
8192 |
16384 |
... |
16777216 |
Visible
Pattern: |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
210 |
211 |
212 |
213 |
214 |
|
224 |
|
Determined by % increase chart: The chart is developed by a 100% increase each hour.
(manually multiply each previous number of bacteria by 2.00, which is all of them plus 100% more)
By doubling each hour, a "pattern" of powers of 2 develops for the number of bacteria.
making the chart easier to compete.
At the end of 24 hours, there are 16,777,216 whole bacteria.
| This chart is very large, and tedious computations are needed to calculate the answer by manually applying the percent of increase. The observation of the "pattern of doubling" is helpful in reducing the manual calculations. This example shows that the use of the exponential function formula will be a time saving solution strategy. |
 "Doubling" means a percent of increase of 100%. "Doubling" means a percent of increase of 100%.
Function:
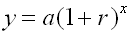 |
a = the initial amount before the growth begins (1)
r = growth rate (100% = 1.00)
x = the number of intervals |
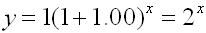 |
as x ranges from 1 to 24 for this problem |
Determined by exponential function: After 24 hours,
y = 1(2 +1.00)24 = 16,777,216 whole bacteria
The pattern from the chart also verifies 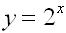 as the function. as the function.
For the graphs below, horizontal axis = end of hour
vertical axis = number of bacteria
|
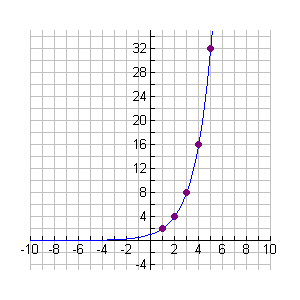 Let's examine the graph of our scatter plot and function. To the left of the origin we see that the function graph tends to flatten, but stays slightly above the x-axis. To the right of the origin the function graph grows so quickly that it is soon off the graph. The rate at which the graph changes increases as time increases. The y-intercept is (0,1).
Let's examine the graph of our scatter plot and function. To the left of the origin we see that the function graph tends to flatten, but stays slightly above the x-axis. To the right of the origin the function graph grows so quickly that it is soon off the graph. The rate at which the graph changes increases as time increases. The y-intercept is (0,1). |
|
 When we can see larger y-values, we see that the growth still continues at a rapid rate. This is what is meant by the expression "increases exponentially".
When we can see larger y-values, we see that the growth still continues at a rapid rate. This is what is meant by the expression "increases exponentially".
Thus, increases very quickly.
|
| |
|

Decay:
Tennis
Tournament |
Each year the local country club sponsors a tennis tournament. Play starts with 128 participants. During each round, half of the players are eliminated. How many players remain after 5 rounds?
|
| Rounds |
1 |
2 |
3 |
4 |
5 |
Number of
Players left
Start = 128 |
64 |
32 |
16 |
8 |
4 |
Determined by % decrease chart: half eliminated = decrease by 50%
There are 4 players remaining after 5 rounds.
 "Half eliminated" means a percent of decrease of 50%. "Half eliminated" means a percent of decrease of 50%.
Function:
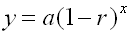 |
a = the initial amount before the decay begins (128)
r = decay rate (50% = 0.50)
x = the number of intervals |
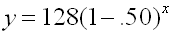 |
as x ranges from 1 to 5 for this problem |
Determined by exponential function: y = 128(1 - 0.50)5 = 4
Verifies that there are 4 players remaining after 5 rounds..
Notice the shape of this graph compared
to the graphs of the growth functions.
The decreasing graph drops quickly,
then levels off as it approaches the x-axis.
If the y-axis was taller, it would
show (0,128) as the y-intercept.
|
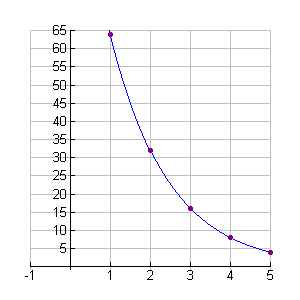
horizontal axis = number of round
vertical axis = number of players left |
|

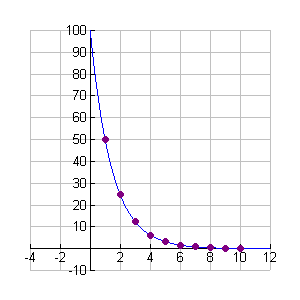
Let's examine the scatter plot and the function.
At x = 0 the y-intercept is 100. To the right of the origin we see that the graph declines rapidly and then tends to flatten, staying slightly above the x-axis. The rate of change decreases as time increases. |
|
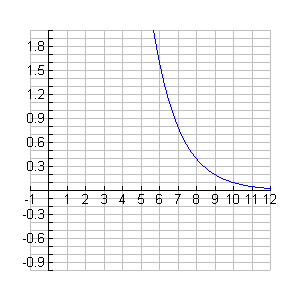
When we zoom in on the flattened area of the graph, we see that the graph does stay above the x-axis. This makes sense because we could not have a "negative" number of grams of DDT leftover. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|